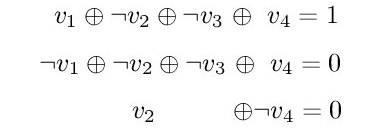|
|
Tutorials and Survey Articles
| ♦ |
|
SAT Basics |
| |
Boolean functions, Shannon expansion, CNF and DNF formulas,
resolution, consensus, and subsumption, Davis-Putnam and DPLL search,
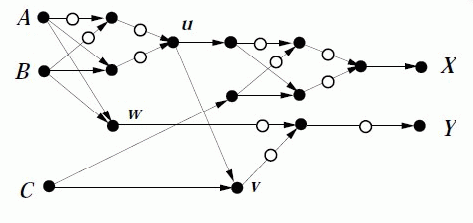
Binary Decision Diagrams, Algebraic representations of Boolean
functions and a decision procedure for systems of multi-linear
equations, And-Inverter graphs and equivalence checking,
Satisfiability Modulo Theories.
|
| |
|
| ♦ |
|
History of Satisfiability |
| |
SAT representations and the applications that made them important.
Effective procedures for each representation. Representations include
Syllogisms, CNF, DNF, BDDs, algebraic representations, and AIGS.
|
| |
|
| ♦ |
|
Conflict-Driven Clause Learning |
| |
CDCL is the paradigm that is mainly responsible for the success of SAT
solvers to date. |
| |
|
| ♦ |
|
Bounded Model Checking |
| |
Bounded model checking arose from the need to verify time-dependent
properties of circuits but is beginning to see applications in other
fields such as medicine where symbolic simulation is now augmenting
traditional concrete simulation.
|
| |
|
| ♦ |
|
Lazy Satisfiability Modulo Theories |
| |
How propositions over a mix of many theories may be connected without
sacrificing soundness, especially through Nelson-Oppen. |
| |
|
|
| |
Other reading material
| ♦ |
|
 |
The above articles on the history of satisfiability, CDCL, and BMC are
taken from the Handbook of Satisfiability. The pdf files on this site are
provided courtesy of the publisher,
IOS Press, the Netherlands. The
handbook has numerous other interesting articles on look-ahead solvers,
local search solvers, branching heuristics, symmetry detection and breaking,
minimal unsatisfiable cores, upper bounds, planning, software verification,
MaxSAT, Quantified Boolean Formulas and more. Check your library for
availability or click the icon to the left for more information about the
handbook.
|
| |
|
| ♦ |
|
 |
The above article on Satisfiability Modulo Theories is taken from the
Journal on Satisfiability,
Boolean Modeling, and Computation. For information about the printed version
of this journal click the icon to the right.
|
| |
|
| ♦ |
|
 |
The Introduction to Mathematics of Satisfiability by Victor
Marek covers many aspects of the topic from Boolean algebras, through
propositional logic, normal forms of formulas, search-based paradigms,
polynomial-time solvable classes, and to knowledge representation and
answer set programming. Click the icon to the left for more
information.
|
| |
|
| ♦ |
|
 |
Boolean Models and Methods in Mathematics, Computer Science, and
Engineering, edited by Yves Crama and Peter Hammer,
covers topics ranging from algebra and propositional logic to learning
theory, cryptography, computational complexity, electrical
engineering, and reliability theory.
Click the icon to the left for more information.
|
| |
|
| ♦ |
|
 |
Boolean Functions: Theory, Algorithms, Applications, edited by
Yves Crama and Peter Hammer, focuses on algebraic representations of
Boolean functions, especially disjunctive and conjunctive normal form
representations. Treats Boolean equations, satisfiability problems, prime
implicants and associated short representations, dualization,
quadratic Horn, shellable, regular, threshold, read-once functions and their
characterization by functional equations, partially defined
functions and pseudo-Boolean functions. Click the icon to the left for more
information.
|
| |
|
| ♦ |
|
 |
Boolean Reasoning by Frank Markham Brown is a good introduction
to the logic of Boolean equations. There are several editions which
differ a bit. Click the icon to the left for the textbook version
available via Springer. There is a small paperback version,
copyrighted 2003, which is available from amazon.com.
|
| |
|
|
|
|
|